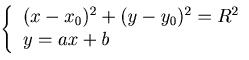Faute de ne pouvoir donner une définition exacte de la théorie du chaos, nous allons, par le biais d'un exemple très simple, tenter d'illustrer ce qu'est cette complexe théorie. Nous étudierons l'évolution des trajectoires d'une boule de billard considérée comme ponctuelle sur une surface plane. Pour différencier plusieurs cas de figure on fera varier la forme de la surface de jeu ainsi que la trajectoire initiale de la boule. Nous allons prendre une équation de départ, à chaque rebond, nous allons devoir recalculer une nouvelle équation de trajectoire.

Prenons tout d'abord une surface carrée et calculons les trajectoires d'une boule considérée ponctuelle. Lorsque l'on calcule les différentes équations qui définissent la trajectoire de la boule rebonds après rebonds on s'aperçoit que les équations se répètent telles quelles au bout de quelques rebonds. Le nombre de rebond après lequel les équations se répètent dépend de l'équation initiale de trajectoire. En effet, pour l'équation initiale y = 2x + 3 : après le sixième rebonds on retrouve exactement l'équation initiale et la boule fait le même trajet encore et encore.

Pour l'équation initiale y = :6x + 1:7, par contre, le nombre de rebond avant de retrouver la même équation est bien supérieur, comme en témoigne la figure suivante.
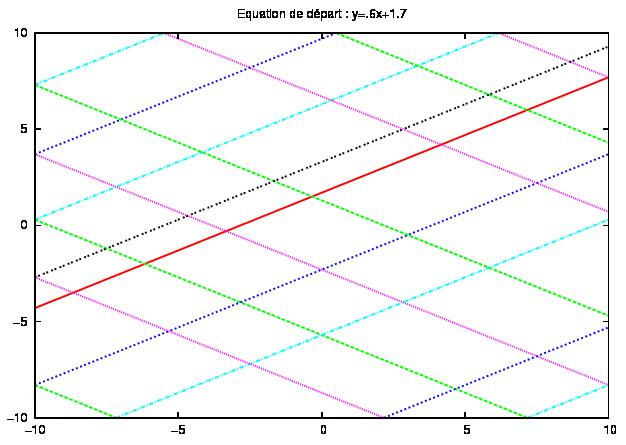
En conclusion on remarque que les trajectoires sont bien ordonnées et que les équations viennent à se répéter, ce qui est conforme à nos attentes puisque nous avons pris une équation de départ connue, assez simple et que nous connaissons parfaitement les équations de la ré ; ce système est déterministe, mais il n'est pas chaotique. Enfin prenons comme forme de billard : un cercle. Suivant la fonction affine que l'on choisit comme équation d'origine, on peut observer la formation d'une rosace qui laissera au centre du cercle une zone parfaitement vierge de forme circulaire et ce, quel que soit le nombre de rebonds effectués ; on appelle cette zone une caustique. La taille de cette zone varie considérablement suivant l'angle que l'on donne à la trajectoire dans l'équation d'origine : plus la première trajectoire passe près du centre de la surface de jeu, plus la caustique est petite ; au contraire si on rapproche la première trajectoire de l'extérieur du cercle, plus la zone sera grande. On observe également l'apparition d'une telle surface vierge de trajectoire lorsque l'on se place dans un demi-cercle.

La présence de cette caustique est synonyme de la non appartenance à l'ensemble des systèmes chaotiques, ce qui semble assez logique car la formation d'une forme géométrique si précise ne semble pas pouvoir être le fruit du hasard, et ne ressemble en rien à un système instable régit par le chaos.
On a répertorié deux cas principaux où on observe des phénomènes chaotiques : le stade d'athlétisme et le cercle tronqué.

Dans ces deux cas lorsque l'on considère les trajectoires avec un nombre élevé de rebonds, on ne voit pas apparaître de caustique, en effet il n'y a aucune partie de la surface aussi petite soit-elle qui ne soit pas coupée par une trajectoire. Et si on fait tendre le nombre de rebonds vers l'infini, le stade ou le cercle tronqué va se retrouver littéralement colorié par l'ensemble des trajectoires de la boule. N'observant pas de zone vierge et à la vue de la diversité "infinie" des trajectoires, on en conclut donc que la trajectoire d'une boule dans ces deux surfaces forme un système chaotique. Pourquoi a-t-on là deux systèmes chaotiques ? La réponse à cette question semble logique : suivant la forme de la surface de jeu. On observe en effet, pour des formes simples, des systèmes non chaotiques ; et pour des formes complexes, telles que les combinaisons de cercles et de lignes droites (stadium, cercle tronqué) qui sont loin d'être des formes géométriques traditionnelles, des systèmes chaotiques.
Nous allons introduire ici un terme qui sera utilisé souvent par la suite : GTK. Il s'agit d'une librairie graphique du langage C, c'est à dire un ensemble de fonctions et de variables, qui est utilisée sous linux pour créer des interfaces graphiques plus conviviales que les consoles shell. GTK est une abréviation de 'Gimp Tool Kit', en effet cette librairie a été créée à la base pour le developpement du logiciel libre TheGimp, le logiciel de retouche d'image. GTK nous permettra de créer les programmes qui illustreront notre rapport, notamment la simulation de lancé de boules de billard mais aussi par la suite pour la réalisation d'un diagramme de bifurcation et pour le tracé du papillon de Lorenz.
Nous avons réalisé un programme à l'aide de GTK 4 qui permet de choisir la forme d'une surface de jeu, le nombre d'itérations voulues, ainsi que l'équation de départ et qui trace les trajectoires rebond après rebond pour pouvoir tester plusieurs cas et observer s'il y a chaos ou pas. Il y a certains problèmes lorsque l'on prend des valeurs trop petites pour le coefficient directeur de la première trajectoire. Ces erreurs sont dues aux capacités limitées des variables lors des calculs, nous nous en excusons. Le code source de ce programme est disponible ici.
C'est la surface de jeu la plus simple. En effet, en partant avec une équation de départ, pour définir la trajectoire, il suffit de :
Petit rappel sur la réflexion : l'angle entre la surface de rebond et la trajectoire incidente doit être le même que celui entre la surface de rebond et la nouvelle trajectoire. Dans le cas du rectangle, les parois sont parallèles aux axes du repère donc pour avoir le nouveau coefficient directeur, il suffit de prendre son opposé. Les équations sont ici de type affine : y = ax + b (a étant le coefficient directeur de la droite et b le point d'origine), ce qui implique qu'après chaque rebond, la pente de la droite va se trouver exactement inversé, d'où le coefficient 'a' va prendre comme valeur '-a', reste à définir le nouveau point d'origine.

Le calcul du point d'origine est très simple il suffit de remplacer les valeurs dans la nouvelle équation au point de départ qui est connu 5 , il ne reste plus qu'à définir l'autre point d'intersection entre le rectangle et la droite d'équation y = ax + b que l'on vient de calculer. Et voilà le résultat :
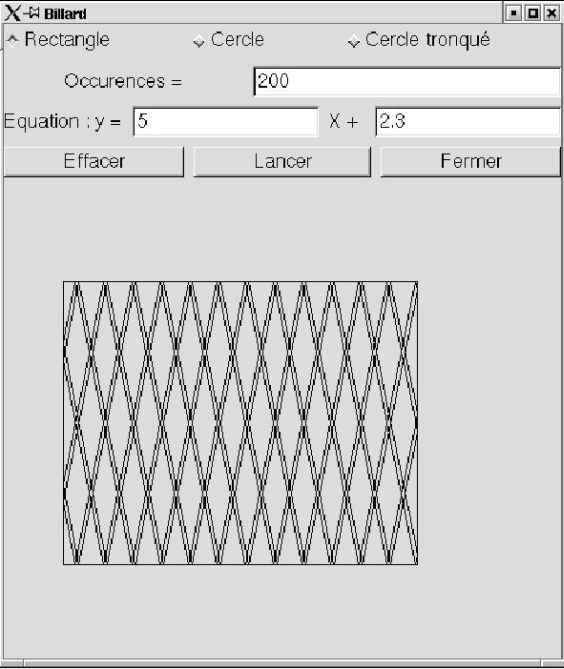
C'est un cas de système non chaotique.
On applique ici une technique similaire à celle du rectangle, mais on ne peut appliquer exactement les mêmes formules puisque là, la surface de rebond sera une courbe. Pour calculer la nouvelle équation de la trajectoire, on va assimiler la courbe en une droite tangente au cercle au point de rebond. On peut alors appliquer le principe de réflexion Mais cette fois ci, la surface de rebond n'est pas parallèle aux axes du repère, on ne peut pas obtenir le nouveau coefficient directeur en prenant l'opposé du précédent comme pour le rectangle.
Sur ce dessin, nous connaissons les points : D, T et C. Nous cherchons les coordonnées du point A. La droite (DA) est parallèle à la droite delta, on cherche donc le symétrique du point D par rapport à la droite (TC) pour pouvoir tracer la trajectoire [TA].

Ensuite il faudra recommencer les calculs en remplaçant A par T et T par D pour obtenir la trajectoire suivante. La méthode consiste à chercher l'équation de la droite (DA) (de la forme y = ax + b) puis à trouver les points d'intersections entre cette droite et le cercle. Il ne reste alors plus qu'à identifier lequel des deux points d'intersection est D, l'autre est le point A que nous cherchons. Le coefficient directeur de la tangente au cercle au point T (delta), est égal à la dérivée du cercle au point T. Nous avons alors le coefficient a de notre équation. En remplaçant le y et le x par les coordonnées de D (car l'on cherche l'équation de la droite de coefficient directeur a passant par D) on obtient alors le b. Il ne reste plus alors qu'à résoudre le système :