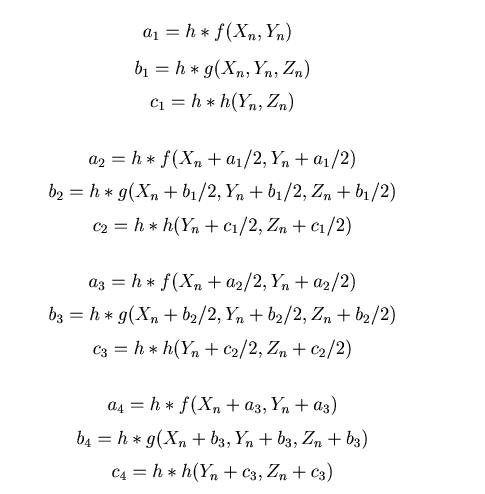L'attracteur de Lorenz
1°) Rappel historique
En 1963, Lorenz publiait ses premiers travaux sur le calcul d'instabilités et de systèmes chaotiques. Il étudia tout particulièrement un système obtenu à l'aide des équations de Navier-Stockes et qui porte aujourd'hui son nom : le système de Lorenz. A l'époque, les calculateurs n'étaient pas très puissants, Pour résoudre son système, Lorenz n'avait pu simuler que 500 itérations. Ainsi, seules quelques boucles de trajectoire avaient pu être décrites. Aujourd'hui, la puissance des calculateurs est telle que n'importe quel ordinateur personnel est capable de calculer des milliers d'itérations instantanément (ou presque).
Nous nous attacherons directement au système sans détailler les simplifications et calculs préalables. Cependant, ce système est obtenu à partir des équations de Navier-Stockes écrites pour un incompressible, dotée de l'approximation de Boussinesq. Nous obtenons alors le système de Lorenz suivant :

Pr,b,r étant des réels constants.
retour au sommet de la page
2°) Résolution
On constate qu'il s'agit d'équation non linéaire à cause du terme xz. Ce système d'équation n'est pas intégrable dans le cas général. La détermination de ce système doit se faire à l'aide de méthode d'approximation (Euler,Runge-Kutta) avec un ordinateur, une fois les 3 paramètres Pr,b,r fixés. Nous avons retenu la méthode de Runge-Kutta.
Méthode de Runge-Kutta : Il existe plusieurs variantes de cette méthode (ordre 3, 4, 5, ...). Nous nous intéresserons à la méthode de Runge-Kutta d'ordre 4 qui calcule la valeur de la fonction en quatre points intermédiaires de la manière suivante :

On a ici un système de la forme :

On obtiendra une approximation de notre système en étudiant les 3
suites :

avec :
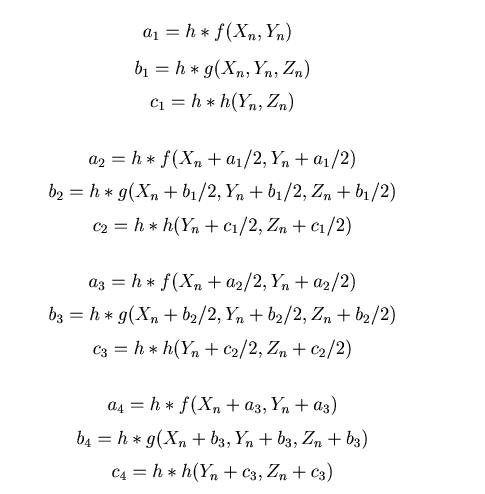
h étant le pas.
Etant donné le nombre important de valeur à calculer (de l'ordre de 100 000) nous allons utiliser un programme codé en C++. Ce programme permet d'écrire dans un fichier les valeurs des 3 suites ci-dessus selon les conditions initiales et les variables définies préalablement.La visualisation des tracés se fait a l'aide du logiciel libre GNUPLOT.
Le tracé a été obtenu avec P r = 10; r = 28; b = 8=3 et un pas (h) de 0.001. Avec les conditions initiales suivantes xo = 10; yo = 10; zo = 20.
attracteur de Lorenz
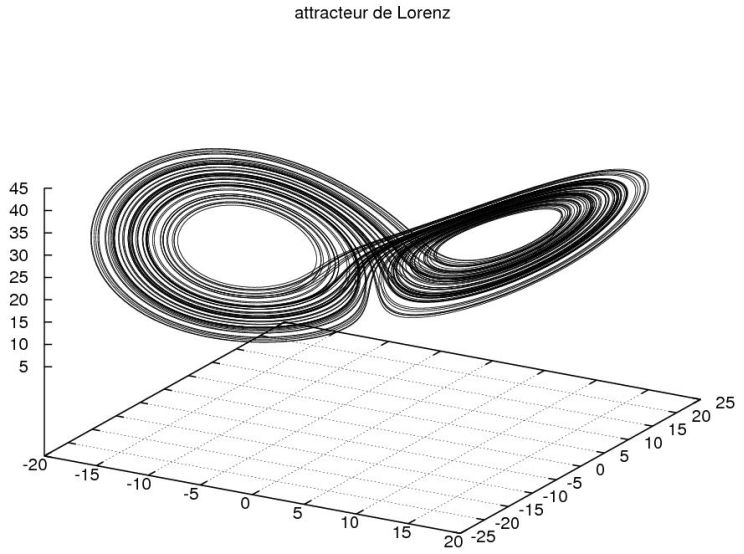
L'attracteur ressemble aux deux ailes déployées d'un papillon. Chaque aile est formée par des séries de cercles concentriques. Les points décrivent plusieurs cercles sur une aile puis bascule sur l'autre sans rythme particulier et sans jamais couper leurs trajectoires.
Pour des conditions initiales très proches (xo = 10,0001; yo = 10,0001; zo = 20,0001) la seconde trajectoire diverge de plus en plus de la première mais va aussi s'enrouler autour des deux boucles.
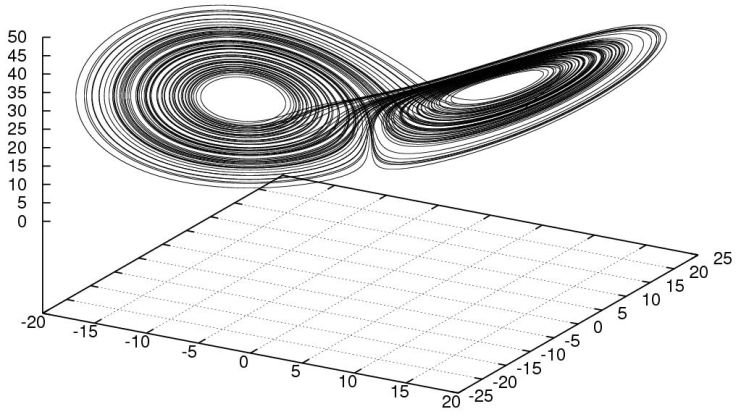
Pour des conditions initiales sensiblement différentes (xo = 50; yo = 50; zo = 60), le premier point apparait loin de l'attracteur puis le rejoint pour ne plus le quitter.
On remarque donc que quelques soit le point de départ le système est irrésistiblement attiré par les deux boucles des ailes du papillon.
On qualifie donc ce genre de figure d'"attracteur étrange". Etrange car les trajectoires ne se coupent jamais et semblent pourtant évoluer au hasard.
Etudions maintenant l'attracteur de Lorenz en faisant varier le paramètre r. En prenant r = 0,5 et comme condition initiale : (xo = 10; yo = 10, zo = 20), on obtient la courbe suivante :

En changeant les conditions initiales (x 0 = 100; y 0 = 100; z 0 = 150) on a le graphique suivant :
On remarque donc qu'avec un r égal à 0,5 le système est attiré vers un même point (0; 0; 0) quelque soit les conditions initiales. Cet attracteur est qualifié d'attracteur fixe. Le système n'est plus chaotique. Avec r = 6 et avec les mêmes conditions initiales que précédemment on obtient les deux courbes suivantes :

Cette fois le système converge vers un point fixe différent selon les conditions initiales. L'attracteur est fixe. Le système n'est pas chaotique.
Afin de mieux visualiser l'importance de la variable r dans la stabilité du système on trace un diagramme de bifurcation : on fait varier r en abscisse et en porte en ordonnée les valeurs x obtenu après un certain nombre d'itérations. On ne fait pas varier les conditions initiales (xo = 0; yo = 0,1; zo = 0). On obtient donc le diagramme suivant :

On distingue 4 cas :
- r < 1 : le système est attiré vers l'origine.
- 1 < r < 14 : le système est attiré vers un point variant selon r.
- 14 < r < 23 : on observe un brusque changement de comportement du système, mais le système tend toujours vers un point dépendant de r.
- 23 < r : le système devient chaotique, cette bifurcation s'appelle bifurcation de Hopf. La particule tourne autour de l'attracteur étrange et les coordonnées calculées deviennent quelconques.
retour au sommet de la page
3°) Programmation
Traçage dynamique de l'attracteur de Lorenz. Grâce au GTK et au langage C, nous avons programmé une application qui réalise le tracé, au fur et à mesure du calcul des points, en partant de conditions initiales variables. Ce projet nous est venu à l'idée en visualisant un écran de veille présent sous linux qui réalise ce tracé.
Source disponible
ici.
Programme exécutable
ici.